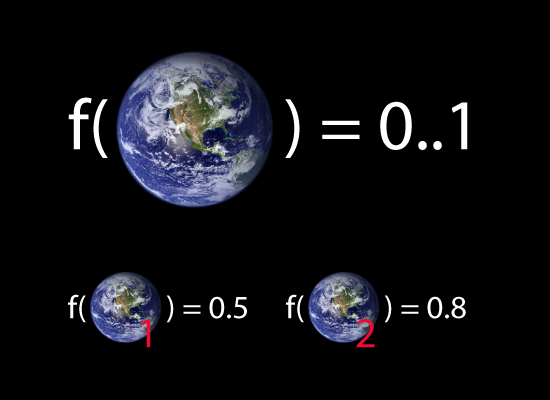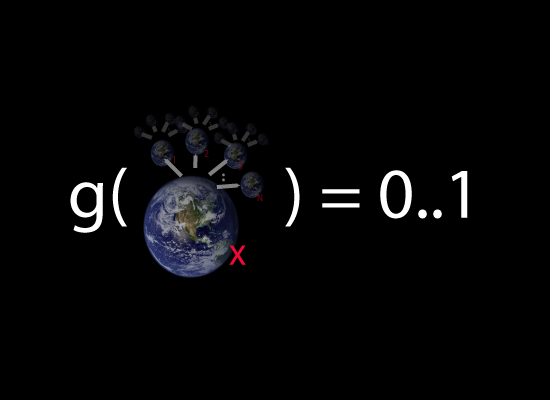A framework for doing your best (long-term)

“The most good for the most people” is the most common everyday description of Utilitarianism. If you want to think long-term then its “The most good for the most people across the most time”

I’d like to take the broader view which simply suggests that “possible worlds” (worlds we can imagine) can be assigned a single (non-unique) summary value.  This allows them to be compared and ordered for utility/good.

My approach will be fraught and won’t be unique, but it will be structured which, in general, makes for good conversation.

Because I don’t want to  focus in on whether happiness/ actualization/number of bunnies or any other specific approach to moral evaluation is the ‘right’ one, I’m simply going to call my function f. The big bonus is that this system will be general enough to apply to assessing the future from multiple perspectives like knowledge, confidence etc and not just good/utility.

f is a function which takes any possible world and assigns it (rather cleverly or maybe magically) a utility (‘goodness value’)  between 0 and 1. Worlds with rating 1 are perfect, worlds with rating 0 are useless and I’d rather be in a 0.8 than a 0.5 if f (for example) rated “worlds I’d rather be in”.

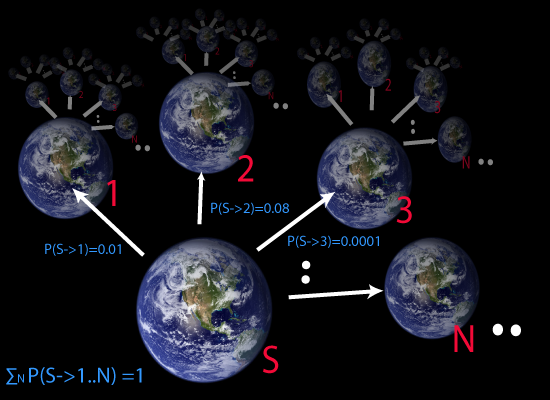
Promising to think long term, we don’t want to act like we can evaluate a world in isolation. We need to importantly look at all of  a single world’s possible futures and their likelihoods. To do this, here’s a diagram of a start world S from which a number of possible worlds can be reached in the next instant.

The idea is that we use f as well as the probability of each of these worlds to work out the expected utility value (E) we will achieve from the successors of S.  Now you might say “this isn’t an issue of probability, it’s an issue of choice” but say that S is a world just a short way into the future from right now and you’ll start to see that even if you yourself could decide everything at S you yourself right now wouldn’t be certain about which choice you would make in the near future. In other words, we can factor in all and any desires to choose any particular world into the probabilities that they will be chosen. The need to do this is even greater when it comes to dealing with the world as a whole (rather than just yourself) and the fact that laws of nature, everyone’s desires and random chance all affect the outcomes.

The method of arriving at the expected utility E is broadly :

E(X)=SUM(X->r=1..N) of (Prob(X->r)*f(r))

….this will assign E(X)=0..1, a calculation of the expected utility of the next world considering the possible of choices.

That is to say that you look at the product of every immediately reachable possible world’s utility  and the probability of that world occurring.

So to really do the trick we need to be able to not just deal with possible worlds in isolation, but “possible world chains” of an arbitrary possible world X and it’s entire possible futures:

The method of combination needs to be such that to evaluate g you evaluate the instantaneous good at world X then combine it with all its successors and their successors etc each multiplied by the probabilities of them occurring. g is therefore a recursive function, but one that can be caused to stabilize if you apply certain limits on how important the future is compared to now.

As an equation:

Try 1: Get the isolated value of the instantaneous world:-

g(X)=f(X)

Try 2: Rate the instantaneous importance of now against immediate future importance:-

g(X)=f(X)*(importance) + (1-importance)*E(X)

Step 3: adapt E to be for all futures rather than just immediate ones:

g(X)=f(X)*(importance) + (1-importance)*SUM(X->r=1..N) of g(r)*Prob(r)

In practice you need to work out importance as a discount function and it should be more than 0.5 for the current world being more important than the combination of all future ones otherwise your search for g(X) may well go on forever. An alternative is to use a heuristic approximation (ie. guessing technique) that looks at a small sample of future possible worlds and estimates their utility and their likelihoods, ignoring the unknown ones.  Doing this well involves techniques I will describe in another post.

In my next basis post I hope to take this model and create specific labels for specific types of worlds with specific configurations of futures. For example a “calamity” might be “a choice where all accessible future worlds  are worse than the current one”. In a final post I will look at strategies for using this approach to optomise in earnest.

For more on discount functions see Kenneth Arrow’s excellent paper where he applies them to Global Warming

For a rather good formal summary see Kripke Structures which were the major influence in writing this.

B